Factor V Leiden and Venous Thrombosis Answers

Question 1

What was the prevalence of the FVL genotype (at least one A allele) among controls? Among cases?

Answer 1

The prevalence of FVL was 22.6% in cases and 3.6% in controls. While 3.2% of cases were homozygous for FVL, there were no homozygotes among controls. (The expected number among controls is 0.05 based on Hardy-Weinberg equilibrium,* corresponding to prevalence of 3.2×10-4 , or 1 in 3117.) Prevalence estimates for both groups are similar to those from previous studies—some of which were based on the same study population.

*p2=163/169=0.964497, p=0.9820881, q=0.0179118, 2pq=0.0351821, q2=3.2×10-4

Question 2

Do you agree that the relative risk of venous thrombosis in OC users was similar regardless of factor V genotype?

Answer 2

Odds ratios of 5.0, 3.7, and 3.8 obtained in this study are essentially the same, given wide confidence intervals. However, two additional points should be considered:

Question 3

What evidence do these data provide for or against interaction between FVL and OC use in venous thrombosis?

Answer 3

In these data,

1. Rge

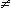
   > Rg + Re – 1, because 30 > 7 + 4 – 1, but

2. Rge

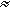
   >Rg x Re, because 30

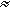
   > 7 x 4

These findings indicate that there is more than additive interaction; the effects of these factors are approximately multiplicative. From a clinical standpoint, the relevant finding shows that women with FVL who use OCs are at much higher risk for venous thrombosis than are other OC users.

Question 4

How does the result of this case-only analysis compare with results of the case-control analysis?

Answer 4

The case-only analysis yields OR case-only

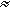
1, suggesting that no interaction exists between FVL and OC use in venous thrombosis under a multiplicative model. Additive or other models of interaction are not excluded by this result. One way to check that genotype and environmental exposure are independent is to compute OR control-only=0.79 in this study.

The case-only design does not yield estimates of the effect of genotype or environmental exposures, or their joint effects.

Question 5

What biases could be introduced by using this approach to estimate person-years at risk for calculating incidence ?

Answer 5

Although the authors refer to this as a population-based study, only the cases can really be considered population-based. The controls were recruited among friends and acquaintances of cases (60%), or partners of other patients at the anticoagulation clinics. Friends may share the same method of birth control, which would tend to inflate the estimated person-years at risk in OC users and thus diminish the estimated absolute risk in this group. (However, the authors noted that prevalence of OC use in this study was similar to that in local population surveys.)

Current OC use was defined as use within 30 days before thrombosis (or index date in controls). Apportioning person-years at risk based on current exposure among controls assumes that OC use patterns were unchanged throughout the course of the study. Subsequent studies have shown that risk of venous thrombosis is greatest during the first year of OC use. Therefore, relevant information for assessing the effect of OC exposures should ideally include dates of initiation and duration of use.

Cases and controls were matched by age, which is critical, because the risk of venous thrombosis increases dramatically with age. However, the analysis was done in unmatched fashion.

Question 6

What is the risk difference associated with OC use in women without FVL? In women with FVL?

Answer 6

Without FVL: 3.0 – 0.8 = 2.2

With FVL: 28.5 – 5.7 = 22.8

The joint effect of the two factors is more than additive.

Question 7

How many women with FVL would have to avoid OCs to prevent one death from pulmonary embolism? How many women would have to be screened to find this many women with FVL?

Answer 7

Excess deaths associated with OC use in women with FVL: (0.57 – 0.11) / 10,000 = 0.46 death / 10,000 py

Number of women with FVL denied OCs: 10,000 py / 0.46 deaths = 21,739 py / 1 death

Number needed to screen to find 20,000 with FVL: 20,000 / 0.05 prevalence of FVL

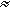
400,000

NNS = NNT/prevalence = (1/risk difference)/prevalence = 1/4.6×10-5/0.05

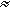
400,000

NOTE: Non-use of OCs by 20,000 women for 1 year is in theory equivalent to nonuse by 10,000 women for 2 years; however, the risk for thrombosis appears to be highest in the first year.